AVL Trees

What if the input to binary search tree comes in a sorted (ascending or descending) manner? It will then look like this −

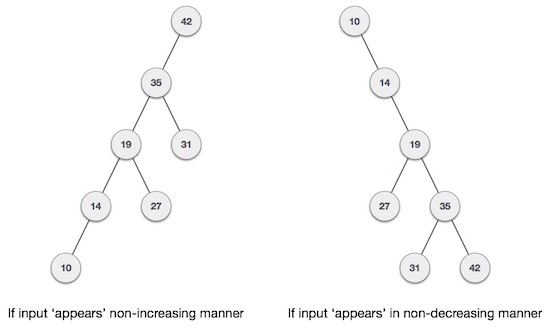
Unbalanced BST

It is observed that BST's worst-case performance is closest to linear search algorithms, that is Ο(n). In real-time data, we cannot predict data pattern and their frequencies. So, a need arises to balance out the existing BST.
Named after their inventor Adelson, Velski & Landis, AVL trees are height balancing binary search tree. AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is called the Balance Factor.
Here we see that the first tree is balanced and the next two trees are not balanced −

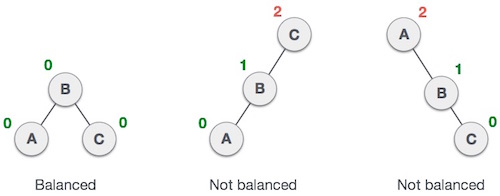
Unbalanced AVL Trees

In the second tree, the left subtree of C has height 2 and the right subtree has height 0, so the difference is 2. In the third tree, the right subtree of A has height 2 and the left is missing, so it is 0, and the difference is 2 again. AVL tree permits difference (balance factor) to be only 1.
BalanceFactor = height(left-sutree) − height(right-sutree)
If the difference in the height of left and right sub-trees is more than 1, the tree is balanced using some rotation techniques.
AVL Rotations
To balance itself, an AVL tree may perform the following four kinds of rotations −
Left rotation
Right rotation
Left-Right rotation
Right-Left rotation

The first two rotations are single rotations and the next two rotations are double rotations. To have an unbalanced tree, we at least need a tree of height 2. With this simple tree, let's understand them one by one.
Left Rotation
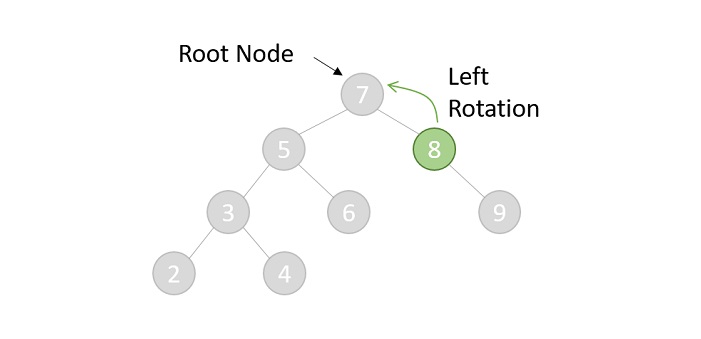
If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation −

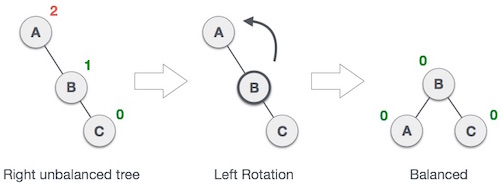
Left Rotation

In our example, node A has become unbalanced as a node is inserted in the right subtree of A's right subtree. We perform the left rotation by making A the left-subtree of B.
Right Rotation
AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation.

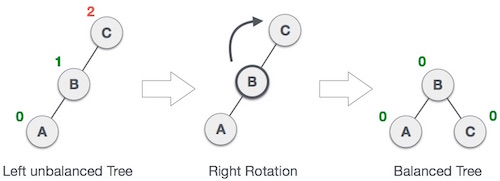
Right Rotation

As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation.
Left-Right Rotation
Double rotations are slightly complex version of already explained versions of rotations. To understand them better, we should take note of each action performed while rotation. Let's first check how to perform Left-Right rotation. A left-right rotation is a combination of left rotation followed by right rotation.
State
Action

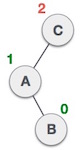
Right Rotation

A node has been inserted into the right subtree of the left subtree. This makes C an unbalanced node. These scenarios cause AVL tree to perform left-right rotation.

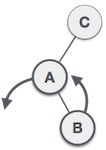
Left Rotation

We first perform the left rotation on the left subtree of C. This makes A, the left subtree of B.

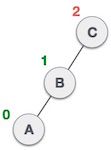
Left Rotation

Node C is still unbalanced, however now, it is because of the left-subtree of the left-subtree.

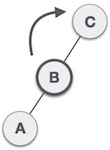
Right Rotation

We shall now right-rotate the tree, making B the new root node of this subtree. C now becomes the right subtree of its own left subtree.

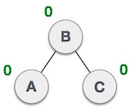
Balanced Avl Tree

The tree is now balanced.

Right-Left Rotation
The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation.
State
Action

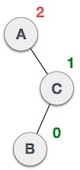
Left Subtree of Right Subtree

A node has been inserted into the left subtree of the right subtree. This makes A, an unbalanced node with balance factor 2.

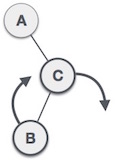
Subtree Right Rotation

First, we perform the right rotation along C node, making C the right subtree of its own left subtree B. Now, B becomes the right subtree of A.

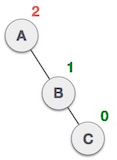
Right Unbalanced Tree

Node A is still unbalanced because of the right subtree of its right subtree and requires a left rotation.

Left Rotation

A left rotation is performed by making B the new root node of the subtree. A becomes the left subtree of its right subtree B.

Balanced AVL Tree

The tree is now balanced.

AVL Trees

推荐阅读更多精彩内容